home..

Natural Looking Procedural Resource Generation

Nathan Reilly / November 2025 (3070 Words, 18 Minutes)

blizzardgame

Overview

In my “blizzard game” project, I’m looking to create a system that procedurally generates resource locations. I want this procedural generation to simulate the natural occurrence of certain resources, with a few key properties:

Ideas

So, here are some ideas that I came up with to solve this problem, in order:

First Attempt - Mapping Perlin Noise to Density

Considerations

As indicated above, the first strategy that I attempted was mapping Perlin noise to the probability that a certain resource spawns. Throughout the process of implementation, there were a few considerations that I needed to resolve:

Where should I generate resources? As of now, no design decision has determined whether the 2D map will be constrained to a limited area. As a result, the solution I currently implement would only be universally viable for future design decisions if it generates resources over a pseudo-infinite map, which would likely be a more complex system involving something like chunking.

Implementing such a generalized solution is impractical at the moment, so I decided to simply generate resources over a defined coordinate bounding box. Thus, the first version of the resource generation system will simply generate resources over the entire map, once, when the player enters the world.

How do I resolve resource spawn conflicts? Since the decided approach will generate resource locations independently for each resource, it’s necessary to consider what happens when two different resources wish to spawn at the same location.

The simple solution I came up with was, for each “competing” spawn location, simply choose randomly from all of the resources that wish to spawn at that location. This approach equally weighs every resource, and thus (based on my intuition) avoids interfering with the natural-looking density change.

Implementation

With these considerations resolved, I had enough of a plan for implementation. I ended up implementing this approach with the following algorithm, as described:

Let \(R_i\) denote the \(i^{th}\) resource type to generate. Initialize a mapping \(D\) which maps grid coordinates \(c\) to the list of resources intending to spawn at that coordinate \(L_c=D[c]\). For each resource type \(R_i\):

  1. For each grid coordinate \(c\) within the map’s bounding box:
    1. If the coordinate is already occupied, continue to the next coordinate.
    2. Retrieve the density \(d\) value using Mathf.PerlinNoise(gridCoordinate).
    3. Generate a random number \(\xi\) between 0 and 1 using a seeded random number generator.
    4. If \(\xi \leq d\), add \(R_i\) to \(L_c=D[c]\)

Then, for each grid coordinate \(c\) in \(D\):

  1. If there is only one resource in \(L_c\), spawn that resource at \(c\).
  2. Otherwise, pick a random resource from \(L_c\) to spawn at \(c\).

Results

This approach was, at best, mediocre. The intended density variation effect (“clumping”) effect was achieved, but there was still something unnatural about the way the resources were generated: First Attempt Results

This is an attempt at generating tree positions, which ideally should somewhat resemble a forest with natural clearings or higher density areas. Unfortunately, it doesn’t seem like that resemblance is achieved here. The issue here is that within areas of equal density, the algorithm essentially degrades to white noise. Resources are placed completely at random. Thus, you get this unnatural-looking generation with excessive clumping and odd emergent computer-like patterns, similar to a TV screen when there’s no signal: White Noise

However, with a bit of further research, I was able to quickly find a significant improvement that could be derived from this existing solution and achieve the intended effect.

Second Attempt - Blue Noise

Background

The key underlying flaw in the above approach, which may be noticed in the “forest” generation attempt, is that within equally dense areas, the resources are simply placed at random. This produces undesirable haphazard clumping and local emergent patterns that don’t resemble a natural environment. To avoid this, then, we would want a more homogenous distribution within these equally dense areas, where resources are usually around the same distance from each other. Perhaps something like this: Blue Noise

The above point generation, where points appear uniformly distributed over the grid, is referred to in computer graphics as “Blue noise” (Huynh, 2019). It’s likely that, by comparing this generation to the white noise above, this one appears much more aesthetically pleasing to you.

While I didn’t research into exactly why this is, it’s likely the case that, in natural environments, things (e.g. trees, rocks, lakes) are often around the same distance from each other. For example, trees and plants too close will compete for resources, but those too far will allow more to grow in between, and thus there’s an emergent optimal distance between them. Thus, spawning resources in a way that imitates this will appear more natural.

Additionally, for gameplay purposes, it is much easier to navigate an environment with more uniformly distributed obstacles. Contrary to white noise, there are no randomly formed walls or clumps that unexpectedly block your path. Similarly, in an actual forest, it’s difficult to picture being suddenly blocked by a clump of trees, or observing a bunch of them forming a straight line. Oftentimes, you’ll be able to travel in any direction you wish without much difficulty.

Thus, my second approach aims to mimic blue noise. Conveniently, the algorithm that generated the blue noise sample above is easily adaptable to my first approach.

Poisson Disk Sampling

The algorithm used for the above-mentioned blue noise sample is known as Poisson Disk Sampling. I’ll explain it briefly below, but this article by Sighack describes it very well and was the source I followed as I implemented it. You can also check out this interactive demo by Jason Davies.

In a uniformly dense grid, this approach defines some minimum and maximum distances between points, \(r_1\) and \(r_2\) respectively.

It begins by initializing a single point at a random position on the grid, and adding it to a stack. Then, it continues to add points that are within the given distance range from the current position at the top of the stack, and that are at least the minimum distance from any other point.

It continues doing this until the grid is filled. This produces a distribution of points such that the distance between the points varies much less than what you’d find in white noise.

With this approach ready, what I had left was to integrate it with the first approach to maintain the density variation/clumping effect that I was looking for.

Integrating the Perlin Noise Density Map

Now, with an approach for blue noise generation, I still wanted to maintain the density variation effect I was looking for, where the density of a resource varies smoothly over different regions. I figured that my original idea of using Perlin noise for the density value would still work well here.

Conveniently, Poisson Disk Sampling is parametrized by a distance range, with the maximum distance often a function of the minimum distance. Due to the way that the points are generated, the average distance to the nearest point is often close to the minimum distance between points.

Additionally, density and the average distance to the nearest point are inversely proportional. This can intuitively be seen by acknowledging that a higher density implies that points are closer together. Thus, the parameterization of Poisson Disk Sampling directly takes density into account. If I want a lower density, for example, I simply increase the minimum distance.

As a result, I figured that given a density \(d\), I can choose the minimum distance between points to be \(r=1/d\).

Finally, I needed to somehow vary the minimum distance parameter \(r\) over different areas, as Poisson Disk Sampling usually instead generates points with a fixed density over the entire grid.

Note that Poisson Disk Sampling produces points in two steps:

In both steps, the value of \(r\) is used relative to either the current active point or the candidate point. Thus, rather than using a fixed value of \(r\) for the entire grid, we instead choose \(r\) to be \(1/D[p]\), where \(D\) is the density map, and \(D[p]\) is the desired density of the resource at point \(p\), as retrieved from the Perlin noise map.

Applied to both steps:

And with that, I now had a full plan for how to integrate the original Perlin noise map with the Poisson Disk Sampling approach, replacing the original method of using the Perlin noise value as a probability.

Implementation

The implementation of the second approach involved changing the way that the locations of each resource type were chosen. However, the rest of the overall algorithm remained unchanged from the first attempt. The following is a high level description of the overall implementation at this point:

Let \(R_i\) denote the \(i^{th}\) resource type to generate. Initialize a mapping \(D\) which maps grid coordinates \(c\) to the list of resources intending to spawn at that coordinate \(L_c=D[c]\). For each resource type \(R_i\):

  1. Initialize a stack \(S\) to contain the currently active points.
  2. Initialize a set \(X\) of coordinates where this resource type has been chosen to spawn.
  3. Choose a random point within the map’s bounding box. Push it to the stack \(S\) and add it to \(A\).
  4. While \(S\) is not empty:
    1. Pop the current active point \(a\) off of the stack \(S\).
    2. Let \(d\) be the density at point \(a\).
    3. For each candidate \(c\) of \(k\) candidates (where \(k\) is some constant integer) randomly chosen within the distance range \([1/d, 2(1/d)]\) from \(a\):
      1. Let \(d_c\) be the density at point \(c\).
      2. If there are no points in \(A\) closer than distance \(1/d_c\) to \(c\), and \(c\) is within the map’s bounding box, then push \(c\) to the stack \(S\) and add it to \(A\).
  5. For each coordinate \(x\) in \(X\), add \(R_i\) to \(D[x]\).

Then, for each grid coordinate \(c\) in \(D\):

  1. If the location is occupied, ignore the coordinate.
  2. If there is only one resource in \(L_c\), spawn that resource at \(c\).
  3. Otherwise, pick a random resource from \(L_c\) to spawn at \(c\).

    Code

    In code, I first needed some way of choosing a random point within a given distance range from a given point. I did so by choosing a random point in an annulus around a given point, using a randomly chosen radius and angle. Since the circumference (and thus the amount of options for points) increases linearly with radius, I chose the radius using linear interpolation between \(r_1\) and \(r_2\) with the value \(\sqrt{\xi}\) rather than \(\xi\) directly:

    private Vector2Int RandomPointInAnnulus(float r1, float r2)  
{  
 float r = Mathf.Lerp(r1, r2, Mathf.Sqrt((float)_rand.NextDouble()));  
 float theta = Mathf.Lerp(0, 2 * Mathf.PI, (float)_rand.NextDouble());  
  
 return new Vector2Int(  
     Mathf.FloorToInt(r * Mathf.Cos(theta)),   
     Mathf.FloorToInt(r * Mathf.Sin(theta))  
 );  
}

Additionally, I also needed a way to conveniently retrieve the resource density at a given point. This was implemented, as mentioned, using Perlin noise:

private float GetResourceDensity(Vector2 position)  
{  
    Vector2 offsetPosition = position + _perlinOffset;  
    return Mathf.PerlinNoise(offsetPosition.x, offsetPosition.y);  
}

Note that _perlinOffset is a randomly chosen offset coordinate, since Mathf.PerlinNoise always produces the same value given the same input.

Finally, I implemented the first part of the algorithm described above (choosing the locations of coordinates) in this function (ReconstructResourceSpawnPositions) within the ResourceLocationGenerator class:

public void ReconstructResourceSpawnPositions()  
{  
    HashSet<Vector2Int> spawnLocationsSet = new(); // X
    Queue<Vector2Int> activePoints = new(); // S
    activePoints.Enqueue(_context.spawnRange.GetRandomPoint(_rand));
      
    while (activePoints.TryDequeue(out Vector2Int cur))  
    {     
        float minDistance = DensityToMinDistance(GetResourceDensity(cur));  
        for (int i = 0; i < ResourceConstants.MaxPoissonDiskRetries; ++i)  
        {  
            Vector2Int candidate = RandomPointInAnnulus(minDistance, 2 * minDistance) + cur;  
            if (!_context.spawnRange.Contains(candidate)) continue;  
      
            float candidateMinDistance = DensityToMinDistance(GetResourceDensity(cur));  
            bool otherPointTooClose = GridAssistant.GetPointsInDistanceRange(candidate, 0, candidateMinDistance)  
                .Any(point => spawnLocationsSet.Contains(point));  
      
            if (otherPointTooClose) continue;  
            // Valid candidate! No other points within minimum distance.  
            spawnLocationsSet.Add(candidate);  
            activePoints.Enqueue(candidate);  
        }  
    }  
      
    ResourceSpawnLocations = new List<Vector2Int>(spawnLocationsSet);
}

Elsewhere, the ResourceLocationGenerator class is used to generate unique spawn locations for each resource type. Then, as described above, these resource locations are combined, and competing resource locations resolved.

Results

![[bluenoise_gen.png]] Second Attempt Results As can be seen in the above screenshot, this worked much more nicely! The forest above looks much more like a naturally occurring forest, with trees generally spawning an equal distance away from each other in equally dense regions. Yet, the clumping effect is maintained, with tree density smoothly varying over different areas.

It can easily be seen how much an improvement it is by comparing it with the first approach’s result: First Attempt Results

Customization

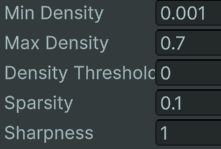
Building off of the nice density-varying resource generation, there was definitely room for customization. Specifically, I wanted a way to vary the manner in which different resources are generated. After playing around with a bunch of adjustments to the above approach, I came up with a decent set of parameters:

The following are some examples of different customizations:

Forest: Tree Generation Parameters Generated Trees

Iron nodes: Iron Generation Parameters Generated Iron Nodes

Coal nodes: Coal Generation Parameters Generated Coal Nodes

After these customizations, I was satisfied with my system. This should easily suffice as a first functional iteration for the procedural generation system. Here’s a combination of all three of the above resources, so you can see what an actual game environment may look like: 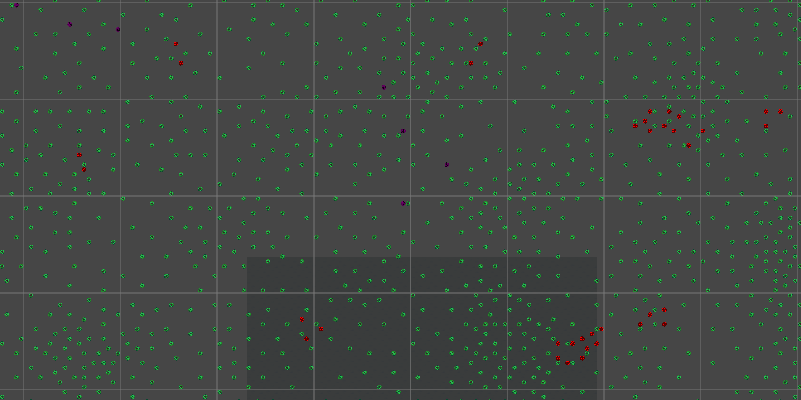Combined Generation Results (Green spots are trees, red spots are iron nodes, and purple spots are coal nodes)

Beautiful…

Further Improvements

There are a few improvements I’d like to make to this system in the future:

However, for now, this is definitely sufficient. With this, I’m currently pretty close to what I’d consider a solid first iteration for my game!

Resources